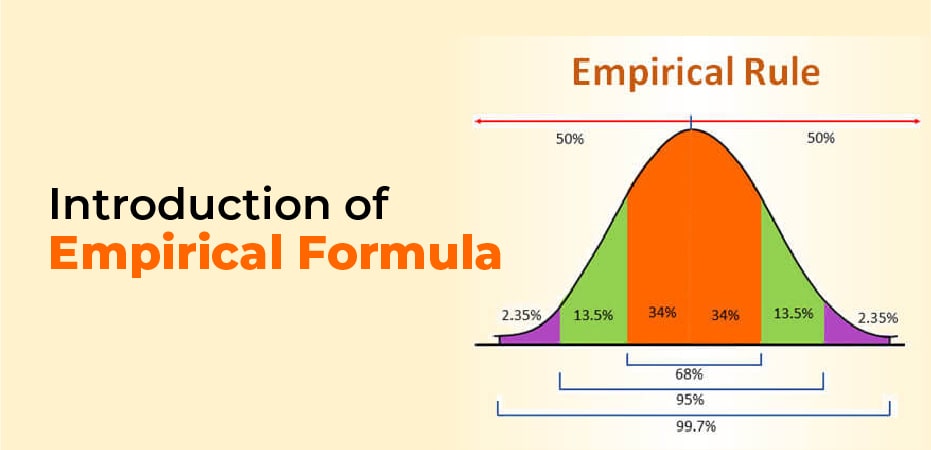
There is a rule called the empirical rule, which is also referred to as the three-sigma rule or the 68-95-99.7% rule. It is a principle of statistics that holds that for a normal distribution 90% of the observed data will fall within three standard deviations (denoted by σ) of the mean or average (denoted byµ).
According to the empirical rule, 68% of observations fall within the first standard deviation(µ ± σ), 95% within the first two standard deviations(µ ± 2σ), and 99.7% within the first three standard deviations (µ ± 3σ).
Introduction of Empirical Formula:
The empirical rule is often used in statistics to forecast the outcome of an experiment. If after calculating the standard deviation and before collecting exact data, it is possible to use this rule as a rough estimate of the outcome of the impending data collection and analysis.
Since this probability distribution can be used as an interim heuristic since gathering the appropriate data may be time-consuming or even impossible in some cases, it is advisable to use it as a preliminary heuristic. It is these considerations that come into play when a firm reviews its quality control measures or evaluates its risk exposure that they should take into account. This is the case with, for example, the widely used risk tool known as value-at-risk (VaR), which assumes that the probability of risk events follows a normal distribution.
An empirical rule can also be used as a rough way to determine if a distribution is “normal”. When too many data points do not fall within the three standard deviation boundaries, this means that the distribution is not normal and it may be skewed or follow some other distribution.
The empirical rule is also known as the three-sigma rule, because “three-sigma” is the definition of a statistical distribution of data within three standard deviations of the mean on a normal distribution.
Empirical Rule: What Does it Mean?
The empirical rule in statistics says that 99.7% of the data within a normal distribution takes place within three standard deviations of the mean. The observable data will be arranged within three standard deviations, 68.8% of which will fall within the 1st standard deviation, 97.5% within the 2nd standard deviation, and 97.5% within the 3rd standard deviation. According to the empirical rule, we can predict the probability distribution for a set of outcomes.
How Does the Empirical Rule Work?
Empirical rules are used to predict what is likely to be the outcome of a normal distribution. An example of how this could be used by a statistician would be to estimate the percentage of cases that fall within each standard deviation. Consider the situations where the standard deviation and the mean are 3.1 and 10. In this particular situation, the first standard deviation would fall between 10 + (3 + 3.2) = 13.2 and 10 – (3 – 3.2) = 6.8. The second deviation would fall between 10 + (2 X 3.2) = 16.4 and 10 – (2 X 3.2) = 3.6, and so forth.
How Does the Empirical Rule Benefit Us?
I believe that the empirical rule is beneficial because it helps to forecast the data in a better way. It is especially important to consider this when we are talking about large datasets and those whose variables are unknown. A specific instance of the empirical rule is in the realm of finance, where it can be applied to the values of stock prices, price indices, and currency logs, which all tend to fall within the boundaries of the bell curve or normal distribution.
